Seno, coseno y tangente
La trigonometría es una rama de la matemática, cuyo significado etimológico es "la medición de los triángulos". Deriva de los términos griegos τριγωνο trigōno triángulo y μετρον metron medida.[1]En términos generales, la trigonometría es el estudio de las funciones seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites
Triángulo rectángulo
Antes de concentrarnos en las funciones, nos ayudará dar nombres a los lados de un triángulo rectángulo, de esta manera: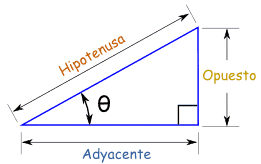
(Adyacente significa tocando el ángulo, y opuesto es opuesto al ángulo... ¡claro!)
Seno, coseno y tangente
Las tres funciones más importantes en trigonometría son el seno, el coseno y la tangente. Cada una es la longitud de un lado dividida entre la longitud de otro... ¡sólo tienes que aprenderte qué lados son!Para el ángulo θ :
Función seno: | sin(θ) = Opuesto / Hipotenusa |
Función coseno: | cos(θ) = Adyacente / Hipotenusa |
Función tangente: | tan(θ) = Opuesto / Adyacente |
Nota: el seno se suele denotar sin() (por la palabra inglesa "sine") o sen(). Aquí utilizaremos sin() pero puedes encontrarte la otra notación en otros libros o sitios web.
Sohcahtoa
Sohca...¿qué? ¡Sólo es una manera de recordar qué lados se dividen! Así:Soh... | Seno = Opuesto / Hipotenusa |
...cah... | Coseno = Adyacente / Hipotenusa |
...toa | Tangente = Opuesto / Adyacente |
Apréndete "sohcahtoa" - ¡te puede ayudar en un examen!
Ejemplos
Ejemplo 1: ¿cuáles son el seno, coseno y tangente de 30° ?
El triángulo clásico de 30° tiene hipotenusa de longitud 2, lado opuesto de longitud 1 y lado adyacente de longitud √3: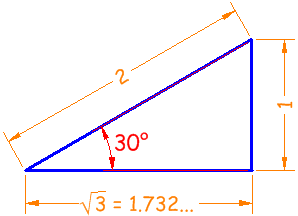
Seno | sin(30°) = 1 / 2 = 0.5 |
Coseno | cos(30°) = 1.732 / 2 = 0.866 |
Tangente | tan(30°) = 1 / 1.732 = 0.577 |
(¡saca la calculadora y compruébalo!)
Ejemplo 2: ¿cuáles son el seno, coseno y tangente de 45°?
El triángulo clásico de 45° tiene dos lados de 1 e hipotenusa √2: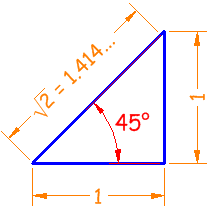
Seno | sin(45°) = 1 / 1.414 = 0.707 |
Coseno | cos(45°) = 1 / 1.414 = 0.707 |
Tangente | tan(45°) = 1 / 1 = 1 |
Ejercicio
Prueba este ejercicio sobre el papel donde tienes que calcular la función seno para ángulos de 0° a 360°, y dibujar el resultado. Te ayudará a entender estas funciones que son bastante simples.Funciones menos comunes
Para completar el cuadro, hay otras 3 funciones donde divides un lado por otro, pero no se usan tanto.Son iguales a 1 divivido entre las tres funciones básicas (sin, cos y tan), así:
Función secante: | sec(θ) = Hipotenusa / Adyacente | (=1/cos) |
Función cosecante: | csc(θ) = Hipotenusa / Opuesto | (=1/sin) |
Función cotangente: | cot(θ) = Adyacente / Opuesto | (=1/tan) |
Seno, coseno y tangente de 30º y 60º
Si dibujamos un triángulo equilátero ABC, cada uno de sus tres ángulos mide 60º y, si trazamos una altura del mismo, h, el ángulo del vértice A por el que la hemos trazado queda dividido en dos iguales de 30º cada uno. Recurriendo al Teorema de Pitágoras, tenemos que la altura es:





Seno, coseno y tangente de 45º





Razones trigonométricas de ángulos notables

Unidades angulares
En la medida de ángulos, y por tanto en trigonometría, se emplean tres unidades, si bien la más utilizada en la vida cotidiana es el Grado sexagesimal, en matemáticas es el Radián la más utilizada, y se define como la unidad natural para medir ángulos, el Grado centesimal se desarrolló como la unidad más próxima al sistema decimal, se usa en topografía, arquitectura o en construcción.- Radián: unidad angular natural en trigonometría, será la que aquí utilicemos. En una circunferencia completa hay 2π radianes.
- Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados.
- Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.
 |  | 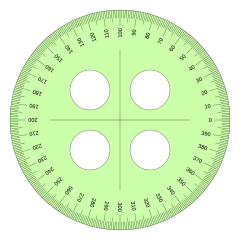 |
| Transportador en radianes. | Transportador en grados sexagesimales. | Transportador en grados centesima |
Razones trigonométricas
El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo
 , correspondiente al vértice A, situado en el centro de la circunferencia.
, correspondiente al vértice A, situado en el centro de la circunferencia.- El seno (abreviado como sen, o sin por llamarse "sĭnus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa,
- El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,
- La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,
 Razones trigonométricas recíprocas
Razones trigonométricas recíprocas - La Cosecante: (abreviado como csc o cosec) es la razón recíproca de seno, o también su inverso multiplicativo:
- La Secante: (abreviado como sec) es la razón recíproca de coseno, o también su inverso multiplicativo:
- La Cotangente: (abreviado como cot o cta) es la razón recíproca de la tangente, o también su inverso multiplicativo:
[editar] Otras funciones trigonométricas
Además de las funciones anteriores existen otras funciones trigonométricas, matemáticamente se pueden definir empleando las ya vistas, su uso no es muy corriente, pero si se emplean dado su sentido geométrico, veamos:
El seno cardinal o función sinc (x) definida:
[editar] Funciones trigonométricas inversas
En trigonometría, cuando el ángulo se expresa en radianes (dado que un radián es el arco de circunferencia de longitud igual al radio), suele denominarse arco a cualquier cantidad expresada en radianes; por eso las funciones inversas se denominan con el prefijo arco,
si:
si:
[editar] Valor de las funciones trigonométricas
A continuación algunos valores de las funciones que es conveniente recordar:


Circunferencia en radianes. Circunferencia en grados sexagesimales.


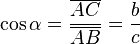


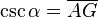

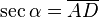

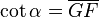




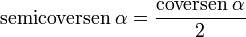
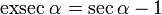
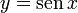

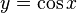
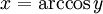
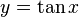

No hay comentarios:
Publicar un comentario